two’s complement overflow有兩種情況會發生
- carry in without carry out
- carry out without carry in
用8 bit signed int為例
-100 + (-30)
1001 1100
+ 1110 0010
------------
1 0000 0000 <- carry bit
C S
= 1 0111 1110
C的位置是carry out(就是我們一般說的carry), S的位置是carry in(就是我們一般說的sign bit)
上面的值是 -130 但是 8bit最小是-128,顯然是overflow
根據上面的規則 屬於 carry out without carry in
再看一個例子
100 + 30
0110 0100
+ 0001 1110
----------------------
0 1111 1000 <- carry bit
C S
= 0 1000 0010
根據上面的規則 屬於 carry in without carry out -> overflow
那要怎麼理解上面的規則呢
這要從overflow可能發生的點看
overflow只有可能發生在
- 正 + 正 => 負
- 負 + 負 => 正
有沒有可能 正 + 正 => 正 還是overflow?
這邊可以用一個圓盤來想,將圓盤分成兩半,藍色區為正(包含0),紅色區為負
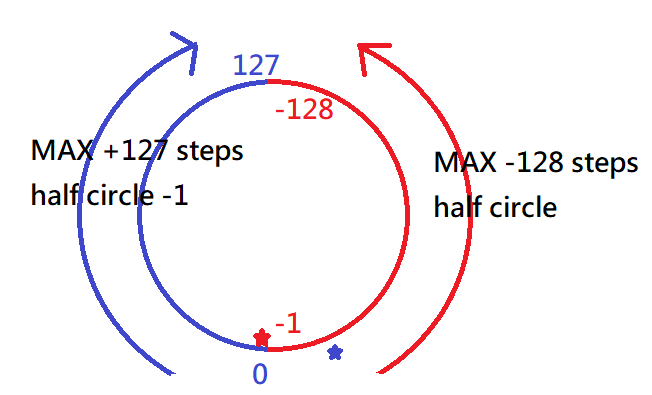
8bit的signed int 是一個循環的圓盤,加法網順時鐘走,減法往逆時鐘走,加法最多(順時鐘)走127步,減法最多(逆時鐘)走128步,因此127 + 127 最多還是負的 (藍色星星標記的地方),-128 + (-128) = 0最多還是正的區域(非負),因此不會有 正+正=正(overflow) or 負+負 = 負(overflow)的情況發生
最後考慮 正 + 正 = 負 & 負 + 負 = 正
正 + 正 0xxx + 0xxx ------- 1xxx <-負 負代表 sign bit = 1,因為 兩個數的sign bit都是0(正), 所以代表有carry in,而carry bit(carry out)也會是0, 因為前一位bit只會有 0 + 0 + 1這種case 負 + 負 1xxx + 1xxx ------- 0xxx <-正 兩個sign bit = 1要加成變成0 代表 1 + 1 + (0 carry in) = 10, 有carry out 1
上面也就解釋了兩個overflow detection的規則了
