palindrome是指一個字串的 string = reverse(string)
而longest palindromic substring則是指找出一個字串中,substring是palindrome的最長substring
這個問題brute force不難想,就是把所有的substring 列出來,檢查是不是palindrome,但是這樣worse case會是O(n^3),因為substring有O(n^2)個,檢查palindrom要O(n)
比較常見的做法是中心點展開法,也就是選取一個點,然後展開看最大可以展到多少長度
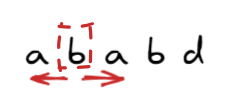
這樣的time complexity為O(n^2),共n個字元做展開,每個字元展開worst case O(n), total O(n^2)
事實上,有更好的方法Manacher’s algorithm time complexity是O(n),可以參考wiki上的說明 https://en.wikipedia.org/wiki/Longest_palindromic_substring#Manacher’s_algorithm
但是Wiki上的說明實在是太難理解了,所以這邊做個整理說明,並給出一些可能的實現
Manacher’s algorithm中文又有人叫馬拉車算法,本質上還是中心點展開法,但是差異在Manacher算法中會把之前走過的展開的資訊做個紀錄,在後面的展開中直接略去從頭開始展開的步驟,直接將整個演算法步數降到O(n)
在處理palindrome時,為了要避免分開處理奇數長度palindrome 或是偶數長度palindrome,一個常見的處理方式是在字串中插入delimeter
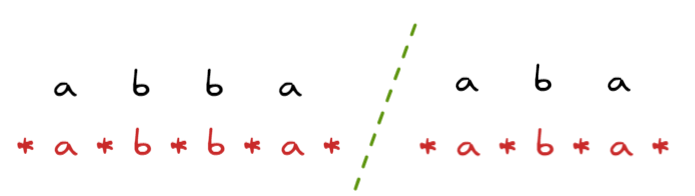
用什麼delimiter都可以,只要不要跟原始string的char衝突就好,加了delimiter後,整個字串的長度一定是奇數,且palindrome也一定是奇數,所以不用擔心要特別偵測偶數的palindrome(偶數palidrome是偵測s[i] == s[i+1],再以i, i+1往兩側展開)
為什麼加了delimiter就保證奇數呢?可以這樣想: N個字元的字串,有N+1個空間,插入delimeter就是N+N+1 = 2N+1 保證奇數,並且觀察以上abba, aba兩個字串的palindrome,可以發現delimeter本身是對稱的,所以也是符合把palindrome空隙插滿,亦即2m+1的情況,因此也是奇數
這邊先看一下其中一個實現方式,此方法參考了 https://www.geeksforgeeks.org/manachers-algorithm-linear-time-longest-palindromic-substring-part-4/ 的思路來實現
std::string lps(const std::string& s)
{
int len = s.size();
int N = 2 * len + 1; //with delimiter
std::vector<int> dp(N);
int C = 1; //current center
int R = 1; //palindrome right index of current center
int maxLen = 1; // max palindrome radius (inclusive)
int maxI = 0; //center index of max palindrome length
for(int i = 1; i < N; i++)
{
int mirrorI = C - (i-C);
int delta = R - i;
if(delta>0)
{
//based on previous information, calculate current palindromic string radius
//also need to take account of information which is out of bound
dp[i] = std::min(dp[mirrorI], delta);
}
while(( i + dp[i] < N - 1) &&
( i - dp[i] > 0) &&
( ((i + dp[i] + 1) % 2 == 0) ||
(s[(i+dp[i]+1)/2] == s[(i-dp[i]-1) / 2])))
{
dp[i]++;
}
//update max radius
if(dp[i] > maxLen)
{
maxLen = dp[i];
maxI = i;
}
//update center
if(i + dp[i] > R)
{
C = i;
R = i + dp[i];
}
}
int index = (maxI - maxLen)/2;
return s.substr(index, maxLen);
}
先理解一下dp內代表的意義
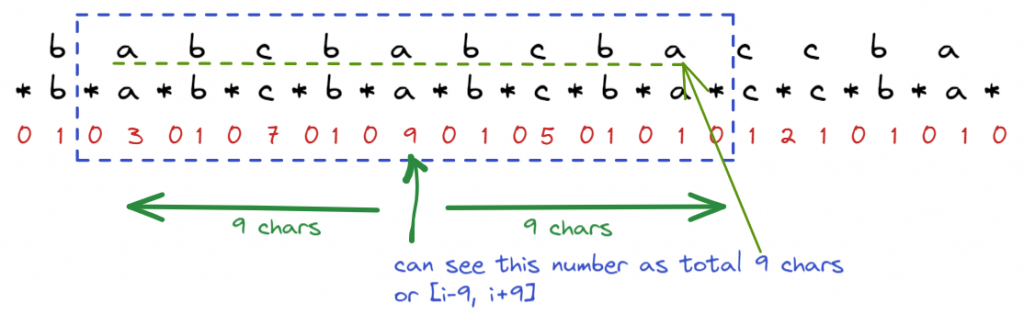
dp中存了走訪的資訊,代表該index [i-j, i+j] 是以該index為中心,最長的palindrome,可以看到圖中的 a dp = 9,代表 該字元 a 往右邊9個與往左邊9個皆相同,也可以發現這個數字對應原來沒有delimiter的字串,剛好以a為中心整個palindrome長度就是9
如果我們可以得到整個dp的值,基本上答案就出來了
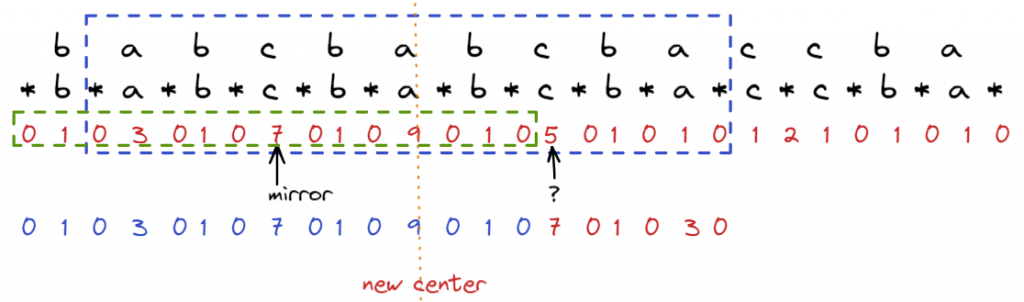
首先看一個範例,以下圖的箭頭處為例,該處字元a 對應的dp值應該是多少呢?
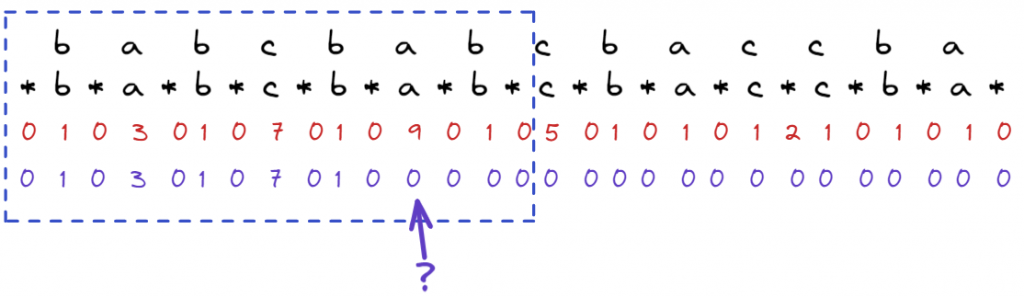
最簡單的想法就是往右走往左走,看看能比對到最長的長度,這樣就要O(n),n個字元就要O(n^2),Manacher的算法說,可以省略一些步驟,方框處是以c為中心點找到最長的palindrome,左右7 chars都對稱,這裡面隱含了一些可利用的資訊
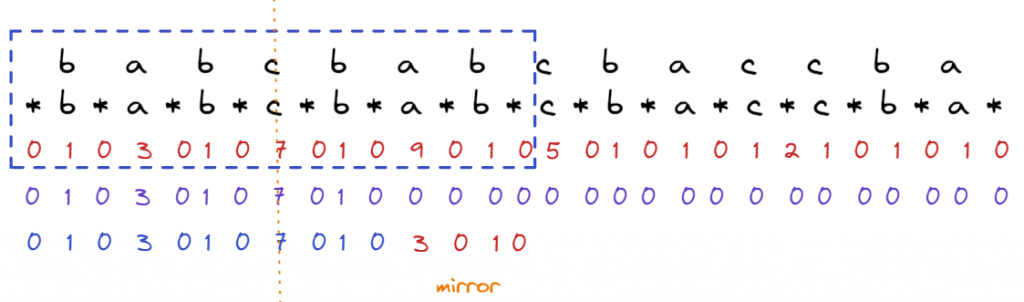
如何找出隱含的資訊,仔細觀察在虛線c的位置,已經找到左右7個對稱,代表在某種程度,左邊看到的世界和右邊看到的世界是相同的, 圖中藍色的數字是已經算好的dp值,下排紅色的數字是從mirror看到的數字,因為對稱,代表在c的方圓內,可以保證兩方在碰到藍色框之內是相同的,藍色框外的世界不知道,這裡我們可以看到至少? 地方的longest match = 3(因為3仍然在方框內)
方框外的資訊就不知道,但是至少我們可以從方框外開始比
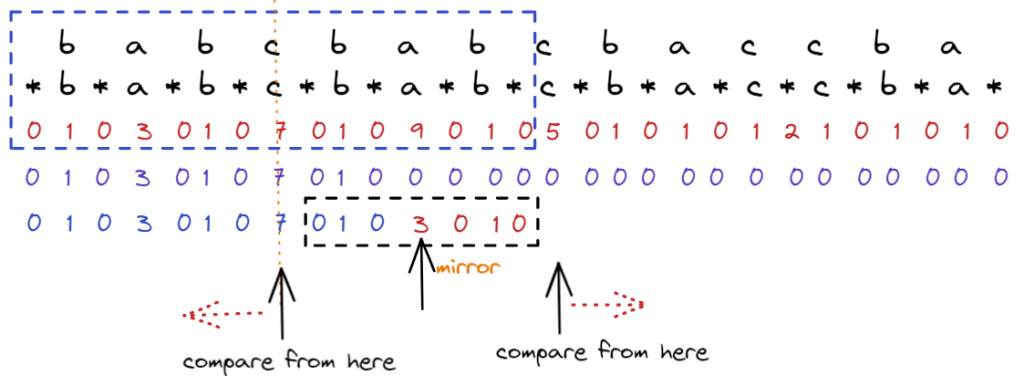
也就是直接跳了3步,直接從j = 4開始比,透過比較完可以知道方框往右可以延伸的地方,必要時更新new center,和new radius
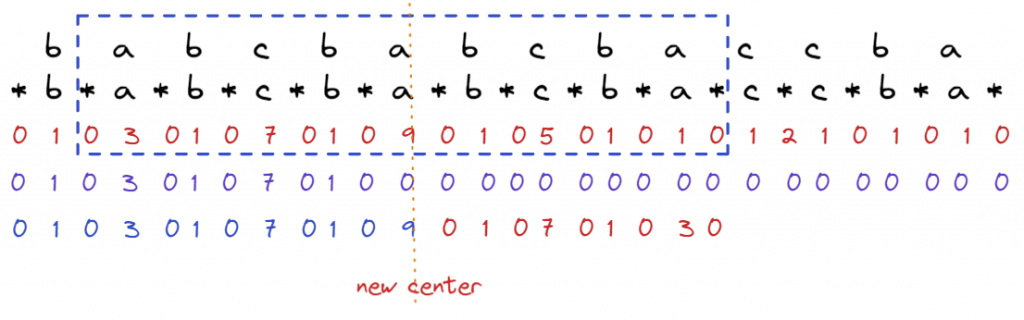
看起來很繁瑣,但是只要掌握住基本的概念,利用可利用的資訊,超出邊界的不能用,邊界外的資訊再另外算的原則,就可以比較好理解
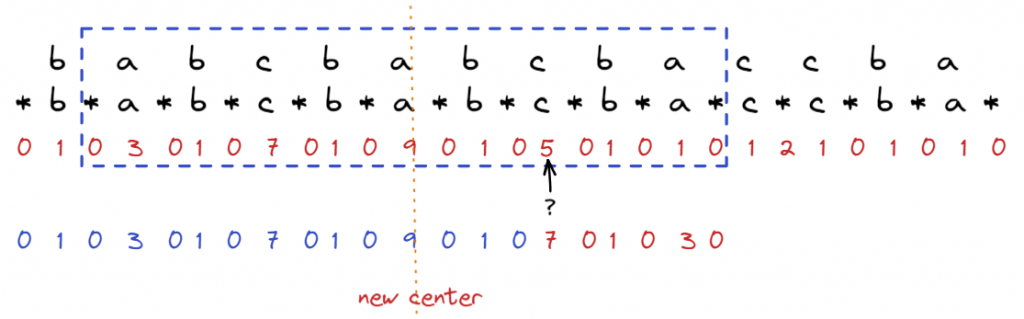
我們再來看圖中?處的值應該是多少,看mirror,應該是7,但是如果仔細看,其實對應的位置走七步是超出藍框邊界的(下圖中綠色框處),因此必須做調整,只能保證到藍框處,也就是5,接著直接從5開始比,比失敗就設定dp = 5
關於time complexity,乍看之下,上面的作法是省略了一些比較,但真的能把n^2降到n嗎?關鍵在於藍框處,會需要做超過一步的比較就代表以新的點為中心,沒有藍框以內的資訊可以用,因此新的比較是從藍框外開始比,如果有比到代表會擴展藍色框的右邊,而藍色框是一路往右的,因此整體的time complexity是O(n)
test case: 這個test case長度約一千多,如果使用一般的做法n^2約做1 million steps

實測step數 Manacher算法對上面的字串 len =1450, steps = 2897
順便附上中心點展開法的一個參考解答(來自於leetcode其他人的submission)
std::string lps(const std::string& s)
{
if (s.size() <= 1) return s;
int maxIdx = 0;
int maxLen = 1;
int i = 0;
while (i < s.size()) {
int start = i;
int end = i;
// expand the window from the end if it's an even palindrome
while (end + 1 < s.size() && s[end] == s[end + 1]) {
end++;
}
i = end + 1;
// expand the window from both sides until it's not longer a palindrome
while (start - 1 >= 0 && end + 1 < s.size() && s[start - 1] == s[end + 1]) {
start--, end++;
}
int currLen = end - start + 1;
if (currLen > maxLen) {
maxIdx = start;
maxLen = currLen;
}
}
return s.substr(maxIdx, maxLen);
}
以上面test case測試,len = 1450,steps = 524902
另外也放上根據wiki 參考,直接使用delimiter作法的實現,和最一開始的實作差別是直接使用加工過的string做計算,不用額外處理index
std::string lps(const std::string& s)
{
int len = s.size();
int N = 2 * len + 1;
std::vector<int> dp(N);
std::string s2(1, '|');
for(auto c: s)
{
s2.push_back(c);
s2.push_back('|');
}
int C = 0;
int R = 0;
for(int i = 1; i < N; i++)
{
if(i > R)
{
C = i;
R = i;
}
else
{
int mirrorI = C - (i - C);
dp[i] = std::min(dp[mirrorI], R - i);
}
int j = dp[i] + 1;
while((i-j >= 0) && (i+j < N) && (s2[i-j] == s2[i+j]))
{
j++;
}
dp[i] = j - 1;
if(i + dp[i] > R)
{
C = i;
R = i + dp[i];
}
}
auto it = std::max_element(dp.begin(), dp.end());
int maxLen = *it;
int index = it - dp.begin();
return s.substr((index - maxLen) / 2, maxLen);
}
總結來說,Manacher算法的核心在如何重複利用先前發掘的dp資訊,並且需要標定藍框的位置,藍框是使得Manacher可以將步數降到O(n)的關鍵,對應程式碼就是C, R變數(center, radius)
Manacher算法其實理解了後並不難,不過理解本身需要沉下心來花一點時間,不能抱著速成心態看。
