string search算法整理 (Knuth–Morris–Pratt algorithm)

這邊列出一個字串算法Knuth–Morris–Pratt algorithm的一個實現，這邊使用的failure function value指最長prefix的最後一個字元的index，-1代表 no prefix match

int search(const std::string& target, const std::string& p)
{
  if(target.size() < p.size()) return -1;
  std::vector<int> v(p.size(), -1);
  int i = 1;
  int j = 0;
  //build failure function stage
  while(i < p.size())
  {
    if(p[i] == p[j]) //matched, update failure function
    {
      v[i] = j;
      i++;
      j++;
    }
    else if(j == 0) //j = 0，不用往前看prefix string，直接放棄比對
    {
      i++;
    }
    else //更新比對基準
    {
      j = v[j-1] + 1;
    }
  }
  i = 0;
  j = 0;
  //compare target string stage
  while(i < target.size())
  {
    if(target[i] == p[j])
    {
      i++;
      j++;
    }
    else if(j == 0)
    {
      i++;
    }
    else
    {
      j = v[j-1] + 1;
    }
    if(j == p.size())
    {
      return i - j;
    }
  }
  return -1;
}

字串的算法看起來很短，但是對於初學者來說非常不容易記憶或理解，主要的原因是死記一定容易忘記，並且failure function value有不同版本的詮釋，如果死記可能會看到不同版本的解法而混亂記憶，理解其中的核心概念非常重要

整個KMP算法的核心思想可以簡單用一句話描述: 比對target string suffix = pattern string prefix，比失敗則退而求其次(再找target string suffix = 次短的pattern string prefix)

在下面的說明中，I代表target string index to compare，J代表pattern string index to compare

KMP的算法可參考 https://en.wikipedia.org/wiki/Knuth%E2%80%93Morris%E2%80%93Pratt_algorithm

原始的字串搜尋算法就是很直觀的將pattern和target一一比對，但是這樣一來worse case就是 O(n * m)，例如 對aaabaaabaaab 搜尋 aaaa

//brute-force
int search(const std::string& target, const std::string& p)
{
  if(target.size() < p.size()) return -1;
  for(int i = 0; i <= target.size() - p.size(); i++)
  {
    for(int j = 0; j < p.size(); j++)
    {
      if(target[i+j] != p[j]) break;
      if(j == p.size() - 1) return i;
    }
  }
  return -1;
}

worse case就是比對到最後fail又要重新開始，雖然在一般情況下，target和pattern的關係不會這麼極端，大部分情況都會early return，在wiki上也有描述到如果是random隨機的情況下，target和pattern要match到n 個字的機率是 26^n(假設charset 是small capital alphabet)，這樣time complexity平均來說就是O(n) 但是這是隨機情形，random也是很極端的case

而Knuth–Morris–Pratt字串搜尋算法可以將worst case降到 O(n)，有些文章寫O(n+m)，不過不影響，主要還是看target string length，另外pattern string length也不大於target string length，如果大於就直接放棄搜尋了

那麼KMP算法是如何將worse case time complexity壓到O(n)呢，最主要就是preprocess pattern string，原始的brute force solution每次fail就pattern match從頭開始，KMP則是可以利用pattern內的資訊，跳過不需重複比較的部分

以 target = ABCDABABCDABD, pattern = ABCDABD為例

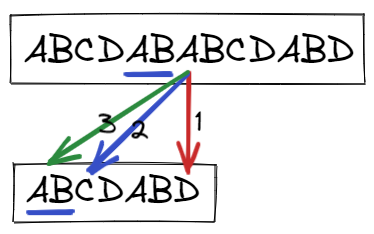
比到index = 6( 0-index)，A對到pattern中的D發現不合，在brute force時此處代表是從index = 0的A起始的，所以會跳到 index = 1的B重新開始比對

但是如果仔細看pattern string，假如已經比到index = 6的D代表target字串從index = 1到index = 5的資訊也已知並且等同於pattern的index 1~5，KMP即是巧妙的利用此信息來去除掉不必要的搜尋步驟，brute force的作法，會移動target index = next，pattern index = 0，而KMP則是只移動pattern index，以上面的例子看就是從紅->藍->綠，乍看之下好像KMP對單一個字元進行了多次pattern跳轉比對，但事實上，因為跳轉是往前跳最多就當前比對pattern位置J的次數，而如果J的數字大，代表I也走了J步才遇到failure，這時候再怎麼跳也頂多跳J步，而此時I的位置不變，所以整個搜尋過程跳轉最多也就是n步

KMP裡面紀錄如何跳轉的資訊用了類似dynamic programming的做法，記錄一個failure function array，那麼failure function如何產生呢，先理解failure function的數字的意義

pattern: ABABABABABABABAA

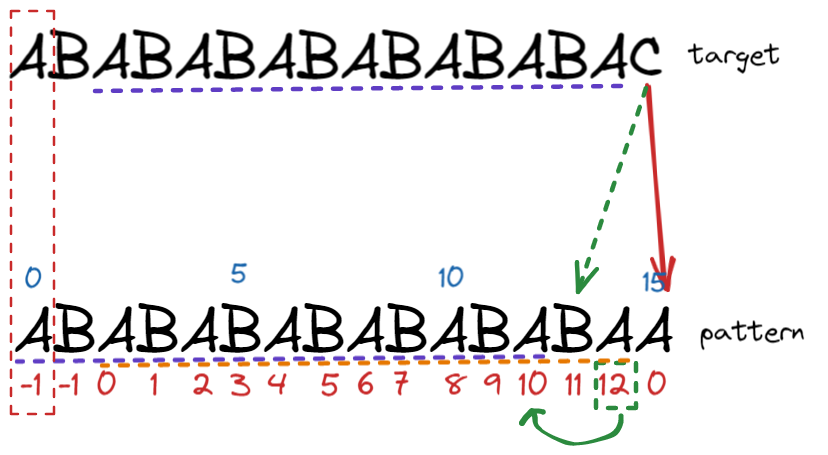
搜尋的target字串為 ABABABABABABABAC

failure function存的資訊即是: pattern中的第J個字元，往前的字串可以找到最長的pattern prefix，suffix = longest pattern prefix

以圖中為例，pattern index = 14 橘線的地方可以找到紫色虛線相同prefix ( index =0 ~ 12)

在比較target string， 從紅色虛線框index = 0開始比，比到index = 15時發現不對，此時代表0-14都是一樣的，而failure function說: index 14往前看和 index 0-12是一樣的，所以C可以直接從index 12 + 1 => index 13開始比(綠色虛線)，如果不一樣就再看failure function，此時target字串雖然不match index=13，但是仍然代表對於pattern match index 0-12是相同的

failure function又說 index 12往前看 跟index0-10是相同的

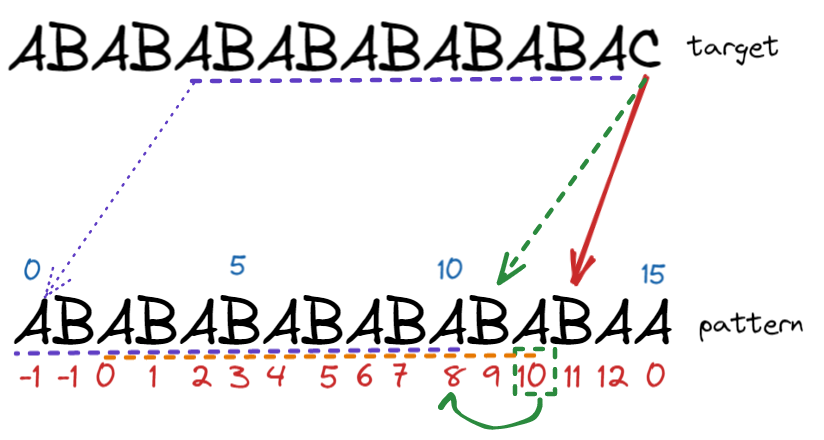
所以比較可以從pattern index 11開始比，即綠色虛線指向處，如此一直重複，直到比對到pattern index = 0，此時退化為原始的判斷，如果連index = 0都不match當然就只能跳過目前的target string char，往後比較了，pattern index = 0也就是重比了

我們可以看到比較的過程，failure function是往前一格查詢，因為當前的字元不match，只能往前一格去找前一格成功比對match的字串，跟pattern字串最長的prefix match，這邊要注意target prefix match比對的起始點不是從頭算，因為我們知道重頭算(前面圖index = 0)紅框處沒辦法match整個pattern，所以要從pattern index = 1之後找prefix match的起始點

以上圖為例，index = 12的A，prefix match是match 從index = 2的字元開始 (index = 2 – 12)，比對pattern prefix(index = 0 – 10)

所以target char != pattern char時就是 J – 1找尋pattern prefix string last index，再從該index + 1繼續比對

前面提到: failure function存的資訊即是: pattern中的第J個字元，往前的字串可以找到最長的pattern prefix，-1代表no match

以上面的例子，index = 0，為A，第一眼看起來好像有prefix match，但是注意前面提到pattern prefix match起始點不是從開頭算，所以此格 = -1

第二個index = 1字元為B，找不到跟pattern 共通prefix，= -1 (AB = AB步算)

第三個index = 2 字元為A, 往前的string 有 BA, A，A跟index = 0 A match，match的prefix string last index = 0，failure function value = 0

index = 4的字元為A，往前的string有BABA、ABA，match pattern prefix ABA，matched prefix last index = 2，failure function value = 2

仔細發現failure function建立的過程，其實就是pattern 中的char和自己比，前面提到的target比pattern的方法可以拿來用到pattern比自己，差別是pattern自己比完還要更新failure function

碰到not match char，就找最長prefix，再更新j，如果match，就更新failure function

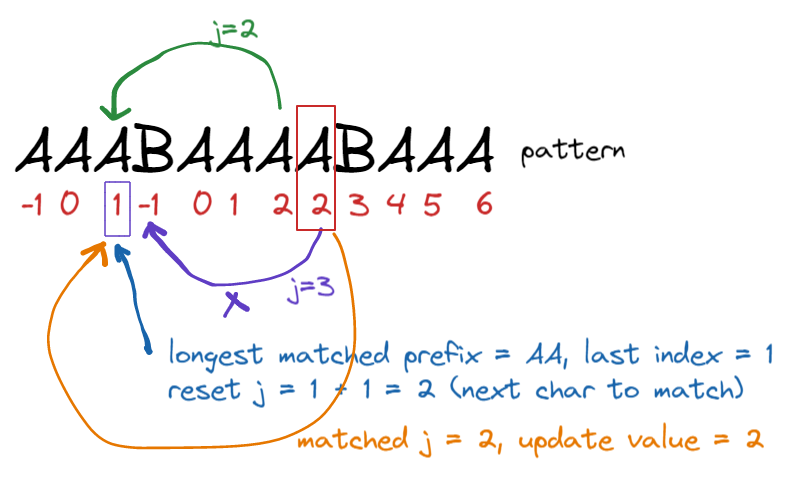
整個實現的細節可以參考最開頭的程式碼

總結來說: 理解 KMP算法的關鍵是

• 查找字串 動pattern index J，不動target index I
• failure function 代表的意義(這篇文章使用的概念是 current suffix = pattern prefix )
• 如何利用failure function減少不必要的比對(如何使用failure function)
• 如何建立failure function

重複利用已知資訊常常是字串算法優化的關鍵，類似的還有Longest palindromic substring，一般brute force 兩個for loop檢查是否為palindrome的作法O(n^3)，好一點的作法是中心點展開也要O(n^2)，但是Manacher’s algorithm可以做到O(n)，有機會再來整理此算法